INTRODUCCIÓN

Cuando a principios de 2002 cambié de área y empecé a trabajar en marketing de cliente, una de las cosas que me contó Pablo, mi jefe de por aquel entonces, fue la forma de calcular el tiempo de vida medio de los clientes a partir de la tasa de bajas de los mismos.

La regla que me enseñó y que es ampliamente usada en cualquier sector donde exista una cartera activa de contrato sujeta a bajas: telecomunicaciones, banca, seguros,... (quedan excluidas las compañías de distribución de agua, luz o gas porque éstas no tienen clientes, solo prisioneros, y por lo tanto en ellas la competencia y la preocupación por estos temas es inexistente), dice lo siguiente:

Dada la tasa de bajas de la cartera, es decir la probabilidad de que un cliente curse baja en un período dado, el tiempo de vida medio o vida media de dicha cartera será el inverso de la tasa de bajas. Dicho de otro modo:

T = 1 / c
Donde T es el tiempo de vida medio y c la tasa de bajas. La denomino c en homenaje a la palabra churn, que es como se le llama a este ratio en telecomunicaciones, donde casi siempre me he ganado la vida. En el sector seguros, que también "disfruté" un tiempo, tienen otro vocablo más refinado: lapse rate, cuyo origen no queda muy claro pues en realidad es un término climatológico.

Poniendo un ejemplo numérico, si la cartera es tal que a lo largo de cada año se da de baja el 20% de los clientes que empezaron el año con nosotros, puede decirse que el tiempo de vida medio de nuestros clientes es de 1 / 0,2 = 5 años. Es decir, en promedio los clientes disfrutan de nosotros (o nos sufren según el caso) durante 5 años.

COMIENZAN LAS SOSPECHAS

Yo era feliz. Había aprendido algo nuevo y la formula pintaba bien: sencilla, elegante y por su proporcionalidad inversa, muy lógica (a mayor tasa de bajas menor tiempo de vida y viceversa). El mosqueo vino cuando el inconformismo por hacer actos de fe me llevó a preguntar a Pablo por el origen del cálculo, y la respuesta resultó algo como:


Fig. 1 Imagen mental provocada por un jefe justificando la fórmula del churn.

Es entonces cuando sospeché que ese prodigio de minimalismo matemático, no debía ser más que una simplificación de "algo" más complejo. Y que si se usaba era: primero porque resultaba fácil, y segundo porque hasta entonces nadie se había quejado.

El tiempo de vida medio es un indicador vital para calcular el valor del cliente (customer lifetime value), estimando los ingresos futuros que generará una cartera a lo largo de su vida útil para acotar el coste admisible de captación de cliente. De hecho es básicamente el tiempo que habría de estar con nosotros la totalidad de una cartera ideal sin bajas, para producir los mismos ingresos que la cartera real sometida a bajas antes de extinguirse*. Solo por este hecho valía la pena indagar un poco.

CÁLCULO EXACTO DEL TIEMPO DE VIDA MEDIO

Considerando una cartera inicial sometida a una tasa de bajas constante a lo largo del tiempo, tendremos una evolución asintótica de la siguiente forma (gráfica azul):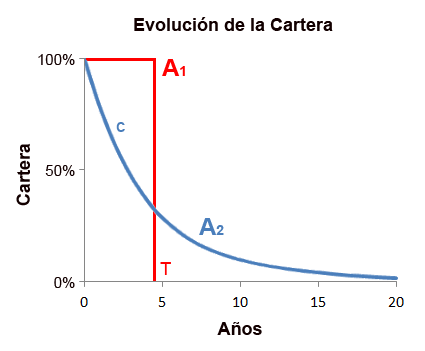


Fig. 2 Evolución de Cartera (gráfica azul) y tiempo de vida medio (T).

La curva lleva a la extinción inevitable de la cartera a largo plazo, ya que no se están considerando nuevas altas que la regeneren. Para conocer la formulación matemática de esa curva basta partir del caso discreto (probabilidad de baja anual), y extenderlo al caso contínuo.

Si la probabilidad de que al cabo de un año un cliente cause baja la denominábamos c, la probabilidad de que siga vivo al cabo del mismo año será p = 1 - c, y por tanto la probilidad de que siga vivo tras n años será:

pn = (1 - c)n
Si ahora consideramos que las bajas son un proceso contínuo que puede darse en cualquier momento, no solo en los valores enteros de la variable temporal (años), la probabilidad de que en un instante t un cliente siga en la cartera será:

p(t) = (1 - c)t
Que es ni más ni menos que la ecuación de la curva de la gráfica. Ahora, con la definición de tiempo de vida medio en la mano* no tenemos más que calcular el valor de T que iguale las áreas A1 = A2, las cuales representan las contribuciones a lo largo del tiempo de cada una de las carteras. Para ello acudimos a un cálculo integral básico: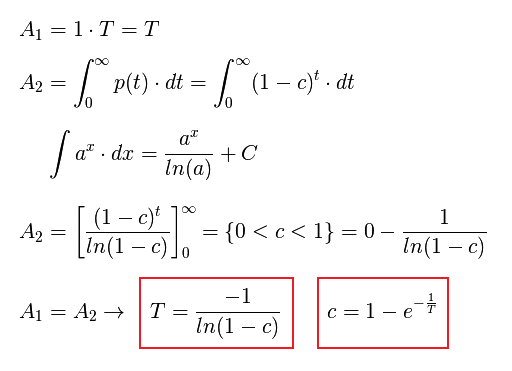


Fig. 3 Cálculo exacto del tiempo de vida en función del churn y viceversa.

Y así tenemos las fórmulas que relacionan de manera exacta el churn y el tiempo de vida medio, que para perplejidad de más de uno he usado sin dudarlo en mi trabajo.

La curva de la Fig. 2 corresponde exactamente al churn del 20% anual del supuesto con que empezaba el artículo, lo que se traduce en el siguiente tiempo de vida medio:

T = -1 / ln(1 - 0,2) = 4,48 años
Que como vemos difiere de los 5 años que estimamos con la aproximación hecha en la introducción, y que emplea el 99,9% de analistas pese a estar cometiendo un error superior al 10% (aceptarían dejar de percibir el 10% de su nómina con la misma alegría?).

Las fórmulas obtenidas son adimensionales, de modo que las unidades del tiempo de vida siempre serán las correspondientes a la tasa de bajas barajada (vida media en años para una tasa de bajas anual, en meses para una tasa mensual,...).


ERROR DEL CÁLCULO APROXIMADO

Y cómo compara el cálculo aproximado que usa (casi) todo el mundo con la fórmula exacta anterior?. Puede verse que para tasas de bajas relativamente pequeñas el resultado de la aproximación T = 1 / c es aceptable, pero para tasas mayores el error se dispara (un churn del 10% marcaría un límite razonable):

c	T aprox. = 1 / c	T exacto = -1 / ln(1 - c)	Error
1%	100,00	99,50	0,5%
5%	20,00	19,50	2,6%
10%	10,00	9,49	5,4%
20%	5,00	4,48	11,6%
50%	2,00	1,44	38,6%
99,99%	1,00	0,11	821,1%

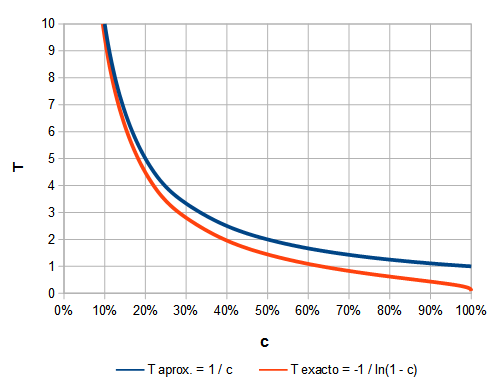
Fig. 4 Cálculo aprox. de tiempo de vida en función del churn vs cálculo exacto.

Mirando la gráfica vemos que la aproximación hace corresponder una tasa de bajas del 100% con un tiempo de vida unidad, lo cual es incorrecto. Un churn del 100% en cualquier período corresponde a un tiempo de vida que tiende a 0.

Esto da lugar a conversiones entre churn y tiempo de vida medio de cliente erróneas en entornos muy dinámicos como es el mercado de las telecomunicaciones, donde una tasa de bajas anual de un 10% es un sueño prácticamente inalcanzable, estando las cifras realistas más en el entorno del 25%. Con valores optimistas de vida de cliente cualquiera cuadra un business case, pero eso sí, que luego se cumpla es otra historia!.

Haciendo series de Laurent o Taylor puede verse que 1 / T es el primer término del desarrollo de c = 1 - e-1/T, lo que demuestra tanto la buena intención como la imprecisión al alejarnos del origen (c = 0⁺) de la fórmula T = 1 / c, oralmente transmitida de generación en generación de marketers y financieros.

DEFINICIONES CORPORATIVAS DE CHURN

En paralelo a todo lo comentado, cada organización o proyecto tiende a tener su propia definición de churn que, si bien está siempre directamente relacionada con el concepto de tasa de bajas visto (que es la genuina definición de churn), no será exactamente equivalente.

El motivo es que se suelen introducir términos relativos a la "cartera media", que implican contemplar en el cálculo no solo bajas sino también las altas que se han inyectado en el período, incluyendo las consiguientes bajas adicionales que éstas puedan generar.

Un ejemplo habitual de estas definiciones creativas de churn sería:

Churn = Sumatorio bajas en el año / Cartera media en el año
La cartera media se suele calcular como el promedio de los cierres en los 12 meses del año, o en ocasiones de la ventana de 12 meses desplazada un mes hacia atrás para modelar mejor las carteras que dieron lugar a las bajas participantes en el cálculo.

No tiene nada de malo la existencia de estos KPI's corporativos pues son significativos y correctos por sí mismos para lo que quiere representarse con ellos (normalmente un indicador de la rotación y tensión a que está sometida la cartera en el mercado).

El problema viene cuando se asimilan estos cálculos a una verdadera tasa de bajas, para convertirlos en tiempos de vida medios de cliente. Hacer esto es incorrecto pues las altas que se produzcan en un período, no pueden en ningún caso influir en la estimación de vida media de una cartera que se encontraba cerrada y bajo observación desde el inicio del período.

Al anterior error se suma el hecho de usar habitualmente la fórmula aproximada de conversión de churn en tiempo de vida, con lo que el resultado es una cifra de difícil interpretación real y de dudosa corrección para obtener el valor del cliente (customer lifetime value), cálculo que normalmente va directo a líneas de presupuestación de ingresos en campañas de marketing o estudios de canal de captación.

Curiosamente este mal uso de las definiciones internas del churn es el día a día en muchas empresas y la Tierra sigue girando, así que no le daremos más vueltas al asunto.

CONVERSIONES DE CHURN PARA DISTINTOS PERÍODOS

Para finalizar quería comentar la forma correcta de trasladar la tasa de bajas o churn medido en un cierto lapso de tiempo a cualquier otro. Es algo muy habitual por ejemplo para anualizar tasas de bajas medidas en un período más corto, y servirá de paso para desvelar otro error de cálculo que de manera continua se comete en el mundo laboral.

Siguiendo con el ejemplo numérico de la introducción, si al cabo de un año he perdido el 20% de la cartera de partida estudiada, cuánto puedo esperar perder en total al cabo de dos años?. Si tu respuesta es un 40% no te preocupes, es incorrecta pero no estás solo sino muy bien acompañado. Para asimilarlo solo tienes que preguntarte ahora qué % de la cartera habrías perdido en seis años... A que no salen las cuentas?.

Para entenderlo pongamos que partimos de una cartera de 1.000 clientes. Si en el primer año perdemos el 20% de ellos, es decir 200 clientes, empezaremos el segundo año con 800 clientes.

Sin más información, hemos de asumir que la tasa de bajas (20% anual) se va a mantener, así que lo esperable en el segundo año es perder de nuevo el 20% de los clientes, pero de los 800 que nos quedan!, no de los 1.000 con que empezamos hace un año. Eso implica perder 160 clientes durante el segundo año.

Así la pérdida total de clientes en los dos años será de 200 + 160 = 360, lo cual representa una tasa de bajas bienal de un 360 / 1000 = 36%, y no un 40%.

La manera más sencilla de realizar conversiones de churn entre un período y cualquier otro, sea mayor o menor al de partida, es verlo en términos de probabilidad de que un cliente siga vivo, es decir, de que no haya cursado baja, en cada período. Así por ejemplo si tenemos la tasa de bajas mensual c1, anualizarla es tan sencillo como hacer el siguiente cálculo:

• Probabilidad de que siga en cartera tras un mes: p1 = 1 - c1
• Probabilidad de que siga en cartera tras 12 meses: p12 = p112 = (1 - c1)12

La tasa de bajas anual será la probabilidad de que haya cursado baja en cualquiera de los 12 meses, o lo que es lo mismo, el complementario a la probabilidad de que siga en cartera tras 12 meses:

c12 = 1 - p12 = 1 - (1 - c1)12
Esta fórmula se puede generalizar para pasar de una tasa de bajas medida en un período de n unidades temporales a un período de m unidades temporales como:

cm = 1 - (1 - cn)m/n   ;   (1 - cm)n = (1 - cn)m
El cálculo soporta cualquier pareja de lapsos temporales, basta plasmar en el cociente m/n la relación entre el período de partida (n) y el que se desea calcular (m). Para el ejemplo del 20% de churn anual tendríamos estas conversiones:

• Bienal: c2 = 1 - (1 - 0,2)2 = 36%
• A seis años: c6 = 1 - (1 - 0,2)6 = 73,8%
• Mensual: c1/12 = 1 - (1 - 0,2)1/12 = 1,84%

~~~

Si este contenido te ha resultado útil, considera realizar una contribución para asegurar la continuidad de esta web. Mantenerla supone un importante esfuerzo, así como un espacio y ancho de banda considerables en el servidor. Es una operación sencilla y totalmente segura.