INTRODUCCIÓN

El siguiente artículo pretende introducir el uso de una herramienta muy conocida en tratamiento digital de todo tipo de señales para un uso muy concreto aplicado a la imagen: la eliminación de tramas repetitivas.

Denominamos 'trama' a una alteración del nivel de luminosidad de la imagen siguiendo un patrón periódico repetitivo que afecta a toda la superficie de la misma.

Es muy típico encontrar este tipo de tramas cuando se lleva a cabo por ejemplo el escaneo de fotografías antiguas en papel pues el soporte de las mismas propiciaba tener esta rugosidad o textura periódica que se transmitía a la imagen.

La herramienta matemática que vamos a emplear es la denominada Transformada de Fourier, o más concretamente su versión aplicable a señales digitales, la Transformada Discreta de Fourier.

UN POCO DE TEORÍA SOBRE LA TRANSFORMADA DE FOURIER

La Transformada de Fourier es una operación matemática que convierte una señal o función en el dominio de una determinada variable o variables (el tiempo, el espacio,...) al dominio de la frecuencia. Se hablará así según el caso de una frecuencia temporal, de una frecuencia espacial,...

No es una operación que altere la señal sino que simplemente nos la muestra en un nuevo dominio. Es algo así como una nueva forma de ver la misma señal, pero que va a tener usos muy intuitivos no disponibles en su estado original que facilitarán enormemente el aprendizaje de ciertas cualidades de dicha señal.

La Transformada de Fourier surgió como una operación sobre funciones o señales contínuas (analógicas), involucrando integrales que no siempre pueden resolverse con facilidad.

Sin embargo, con la aparición de las señales discretas (digitales), la aplicación de la Transformada de Fourier se simplificó enormemente y se convirtió en un mero cálculo matemático que siempre tiene solución, estando tan solo limitado por la potencia de cálculo de la máquina y la complejidad de la señal discreta en cuestión (básicamente su longitud).

Surge así el concepto de Transformada Discreta de Fourier o Discrete Fourier Transform, en adelante DFT. La expresión de la DFT de una señal digital, compuesta ésta por una serie de muestras x_n para N valores de n comprendidos entre 0 y N-1 es la siguiente:


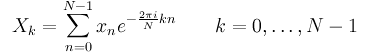
Fig. 1 Expresión matemática de la DFT.

La DFT es reversible de modo que podemos volver a obtener las muestras de la señal discreta original a partir de las muestras de su DFT mediante la Transformada Discreta Inversa de Fourier o IDFT:


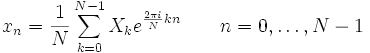
Fig. 2 Expresión matemática de la IDFT.

Convertir una señal dada al dominio de la frecuencia es clave para analizar sus características espectrales, pero igualmente puede usarse, como de hecho vamos a realizar en este tutorial, para realizar transformaciones sobre la imagen una vez ésta ha sido representada en este nuevo dominio. Hechas estas transformaciones recuperaremos la imagen original mediante la aplicación de la IDFT.

Las siglas FFT significan Fast Fourier Transform, es decir, Transformada Rápida de Fourier, y se trata ni más ni menos que de un algoritmo optimizado para calcular en un menor tiempo la DFT pero el resultado es exactamente el mismo. En adelante nos referiremos por lo tanto a la denominación FFT ya que haremos uso de dicho algoritmo.

Igualmente denominaremos IFFT a la Transformada Rápida Inversa de Fourier que nos permitirá devolver la señal a su estado original.

Las formulaciones descritas de la FFT se refieren al caso de señales unidimensionales. Para el tratamiento de imágenes que nos ocupa existen formulaciones equivalentes en dos dimensiones.

EJEMPLO PARA ENTENDER DE QUÉ VA TODO ESTO

Sin entrar en honduras sobre lo que significa cada uno de los términos de las expresiones vistas (que a algunos nos acompañaron en varios años de carrera) diremos que la FFT es una transformación que permite conocer el contenido en frecuencia de una señal, es decir, la representación de su espectro de frecuencias.

Para que esto se entienda tomemos primero un ejemplo de señal más intuitiva que la imagen: el sonido. A partir de las muestras de un sonido digitalizado, la FFT nos informará acerca de su contenido en cada una de las frecuencias del espectro sonoro.

Así, si el sonido era grave la FFT tendrá una amplitud importante en la parte de bajas frecuencias del espectro. Del mismo modo si el sonido era agudo, la FFT tomará valores altos para las frecuencias altas.

Con la imagen pasará lo mismo, pero la interpretación es algo menos intuitiva pues en ella estaremos hablando de una frecuencia espacial y además dispuesta en dos ejes pues se trata de una señal bidimensional.

Así la FFT de una imagen presentará amplitudes importantes en las bajas frecuencias si la imagen tiene variaciones lentas de luminosidad (es decir, presenta poco detalle). En cambio su FFT tendrá un contenido importante de altas frecuencias si la imagen tiene variaciones rápidas de luminosidad (mucho detalle).

En el apartado propiamente de tutorial podremos ver con claridad el aspecto que presenta la representación de la FFT de una imagen, así como la intepretación de estas altas y bajas frecuencias.

Y POR QUÉ PARA ELIMINAR TRAMAS?

Una de las propiedades de la FFT y de la Transformada de Fourier en general es que presenta picos muy acusados si la señal contiene inmersa en ella comportamientos periódicos repetitivos. Estos picos o deltas aparecerán localizados precisamente en la frecuencia del comportamiento periódico y en sus armónicos.

De este modo, una imagen que presente una trama periódica en toda su superficie con un período espacial (separación de píxels) constante, aparecerá muy bien reflejada en la FFT como unas cuantas zonas estrechas pero de gran amplitud relativa al resto que las harán fácilmente identificables.

Solo necesitamos poder actuar sobre esas zonas específicas para cancelarlas, y aplicar luego la IFFT para volver de nuevo al dominio del espacio pero ya con la trama periódica sustraida de la imagen.

PASOS PARA ELIMINAR TRAMAS MEDIANTE FFT

Para el tutorial me he basado en un tutorial de un tal Roland Wyant encontrado en una recopilación de utilidades y que puede leerse en Using the FFT filter to remove photographic paper texture, es decir 'Uso del filtrado FFT para eliminar textura del papel fotográfico'.

Una versión más actualizada de dicho tutorial en el que se proporciona una acción de Photoshop para automatizar los pasos puede obtenerse en el artículo FFT Filter with Photoshop Action.

Para la implementación de la FFT emplearemos un plugin de dominio público para Photoshop programado por Alexandre V. Chirokov.

Partiremos de cualquier imagen que presente un tramado periódico en luminosidad. Es importante saber que la FFT no puede restaurar información si ésta no está presente en la imagen de partida. La FFT solo va a liberarla del patrón periódico de luminosidad pero la información ha de estar ahí.

Por lo tanto no tiene sentido probar este algoritmo sobre imágenes que tengan una textura opaca superpuesta a la original ya que en ese caso se ha perdido la información de la imagen original pues ésta ha dejado de ser visible en los puntos de solape.

Por cortesía de avi_y_lau del foro Ojo Digital, disponemos de un escaneo de una antigua fotografía que presenta un claro granulado periódico debido al papel:


Fig. 3 Imagen con trama periódica por eliminar.

Los pasos a seguir son los siguientes:

1. Instalamos en Photoshop los plugins para realizar la FFT/IFFT de una imagen. Es el link llamado 'Download RGB version of FFT/IFFT Photoshop plugin' que hay en 2D Fast Fourier Transform plugin for Adobe Photoshop. Puede bajarse igualmente de mi propia web desde FFT/IFFT Photoshop plugin. Se trata de dos plugins que se instalarán del modo normal en PS, son la última versión de julio de 2008.
   


2. Una vez instalados en PS hacemos: Filtro → Fourier Transform → FFT RGB, obteniendo la representación de la imagen en el dominio de la frecuencia:
   
   
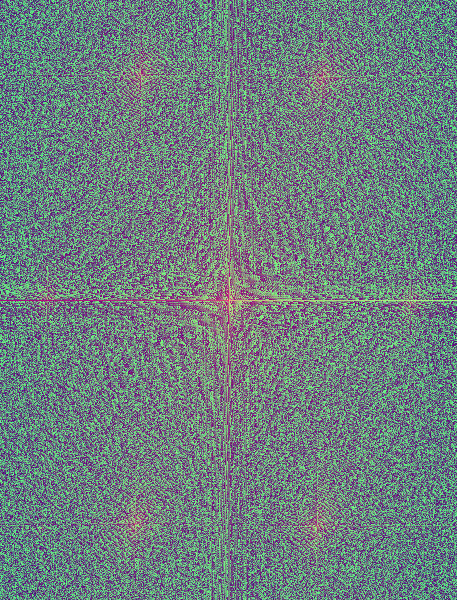
   Fig. 4 FFT de la imagen analizada.
   
   El aspecto de la anterior imagen es un tanto extraño pues en realidad no representa nada obvio: lo que vemos es una imagen compuesta donde en el canal G se ha calculado la amplitud de la FFT, y en el canal R la fase de la misma (la FFT es una señal compleja que tiene por tanto módulo y fase).
   


3. Así acudimos a la pestaña de Canales y seleccionamos el canal G para visualizar la amplitud de la FFT obteniendo:
   
   
   Fig. 5 Amplitud de la FFT de la imagen analizada.
   Ésta es la representación verdaderamente interesante de la FFT, en ella el centro de coordenadas representa el nivel de contínua o frecuencia 0 de la imagen original, representando los dos ejes respectivamente los ejes de frecuencia espacial en X e Y.
   
   El nivel de gris representa la amplitud del módulo de la FFT, cuanto mayor sea el nivel de gris más amplitud.
   
   Los puntos más brillantes corresponden a las deltas o picos correspondientes a los armónicos de la información periódica que aparezca en la imagen, o sea el tramado que queremos eliminar. De no haber ninguna información periódica, no aparecería ningún pico identificable.
   
   Podemos ver que los picos están muy separados entre ellos y respecto al centro; esto es debido a que se trataba de un patrón de alta frecuencia (bajo período espacial). En imágenes con patrones de mayor tamaño, los picos serán más numerosos y difíciles de identificar con lo que el proceso será más trabajoso.
   


4. Puede ser interesante contrastar aparte una copia de la anterior visión para identificar mejor deltas de menor amplitud que se nos pudieran escapar, como en este caso son los puntos más exteriores que son menos visibles, y además para hacernos una idea de la región de influencia de las componentes a eliminar:
   
   
   Fig. 6 Amplitud contrastada de la FFT de la imagen analizada.
   


5. Podemos identificar más claramente 6 puntos muy intensos y otros 4 de menor intensidad. Los anularemos pintando sobre ellos con un pincel negro o gris. Es con esta acción con la que estamos por primera vez alterando la imagen a través de la edición directa de su FFT.
   
   CUIDADO: NO PINTAR EN NINGÚN CASO SOBRE LA ESTRELLA CENTRAL, ya que como se ha comentado el centro de coordenadas corresponde al nivel de contínua de la señal, o sea en este caso la luminosidad media de la imagen. En caso de anularlo llevaríamos ésta prácticamente a negro.
   
   Se tiene la siguiente imagen tras anular los puntos identificados:
   
   
   Fig. 7 Eliminación de las componentes periódicas de la FFT.
   


6. Ahora nos aseguramos de volver a activar los 3 canales seleccionando RGB en Canales, y hacemos la IFFT: Filtro → Fourier Transform → IFFT RGB, obteniendo la imagen limpia del tramado, pero en BN pues esta implementación de la FFT trabaja solo sobre la luminosidad:
   
   
   Fig. 8 Imagen en luminosidad con tramado eliminado.
   


7. No es problema no disponer de la componente de color, acudimos a la imagen inicial y colocamos la recién generada en una capa encima de la original, usando el modo de fusión de Luminosidad para coger de ella solo la luminosidad y la croma de la original:
   
   
   Fig. 9 Imagen final con tramado eliminado.
   

El resultado es muy bueno. Para apreciar mejor la comparación ponemos una porción de la imagen original frente a la resultante, pudiendo comprobar como todo el patrón periódico ha desaparecido y no solo no se han perdido texturas sino que la eliminación de la trama permite identificar las existentes con más calidad:


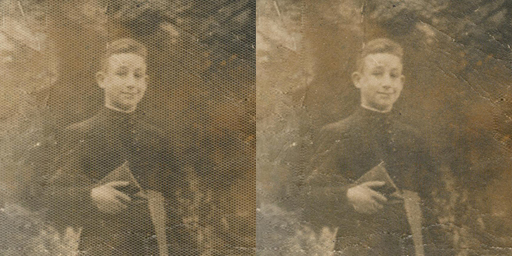
Fig. 10 Comparación antes/después del destramado.

Este hecho es propio del concepto de la FFT, muy diferente al de los algoritmos de eliminación de ruido por ejemplo. Aquí la imagen apenas se ve alterada ya que discriminamos con gran precisión qué partes de la información están provocando el patrón periódico, y solo actuamos sobre ellas.

Se me ocurre que podría cuantificarse de una forma aproximada la pérdida de información máxima sufrida como la relación existente entre la suma de áreas de las zonas pintadas en la Fig. 7 y la superficie total de la imagen.

Deterioro que en cualquier caso se ve compensado con creces con la mejora que supone librarse del tramado. Es además una pérdida de calidad distribuida en toda la imagen por lo que percibirla se hace aún más complicado.

Tras este procesado la imagen estaría ahora lista para iniciar el proceso normal de edición.

NOTAS:

• La versión actual del plugin FFT está preparada para funcionar con imágenes de 8 bits y de un máximo de 4800x4800 píxeles, es un detalle a tener en cuenta.
• En la imagen resultante de las Figs. 8 y 9 pueden verse unos efectos de bordes indeseables en forma de bandas, en este caso a los lados. Este hecho se soluciona sin problemas añadiendo unos 100 píxels de borde gris neutro a la imagen original. Borde que albergará las irregularidades para ser finalmente desechado.

MÁS EJEMPLOS

A continuación vamos a usar la FFT para eliminar un patrón geométrico de bandas diagonales causado por las interferencias en la cámara de las antenas situadas en la azotea de un rascacielos de Nueva York.

La imagen original pertenece al forero Ender de Canonistas, y puede observarse el resultado de la transformación pasando el ratón por encima de la misma:


Fig. 11 Comparación antes/después del destramado (pasar el ratón por la imagen).

De nuevo el resultado es muy bueno. El patrón diagonal desaparece por completo, no solo no afectando al resto de texturas sino que las hace más visibles al eliminar la interferencia.

En este caso se añadió previamente un borde gris 128 para evitar el efecto de bordes comentado en el tutorial. El mapa de puntos anulados en la constelación de la FFT fue el siguiente:


Fig. 12 Eliminación de las componentes periódicas de la FFT.

En este otro ejemplo una foto antigua de José Antonio Grandio tiene un tramado periódico apto para mejorar aplicando la FFT:


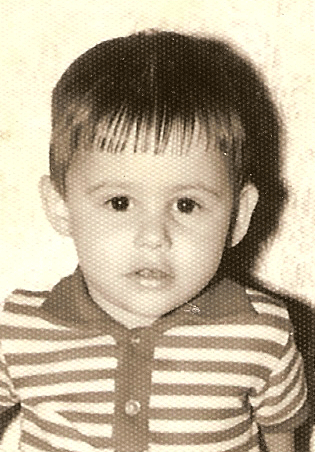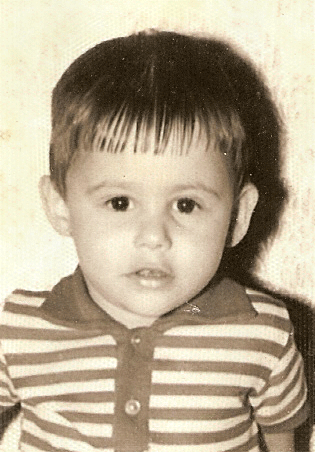
Fig. 13 Comparación antes/después del destramado.

Curiosamente el destramado introduce o enfatiza trama en algunas zonas que no lo tenían en la imagen original (ver zona circundante a la cabeza por el lado izquierdo). No habría más que tomar la parte más adecuada de cada imagen para solucionarlo.

La constelación FFT usada para lograr tal resultado fue la siguiente:


Fig. 14 Eliminación de las componentes periódicas de la FFT.

FFT PARA DETECTAR REDUCCIÓN DE RUIDO SOFTWARE

Aunque el tutorial se centra en la eliminación de tramas periódicas mediante la FFT, he querido aprovechar para comentar otro uso de la FFT: la detección de reducciones de ruido por software.

Esto es de aplicación por ejemplo a la hora de saber si nuestra cámara realiza algún tipo de procesado "clandestino" sobre los datos antes de guardar el archivo RAW, típicamente para reducir ruido. Ello provocaría que la cámara pareciera tener un mayor rango dinámico del que realmente tiene, y a costa de perder detalle o nitidez, ya que ningún método de procesado para reducir ruido que actúe directamente sobre los datos de una imagen es capaz de dejar inalterada la textura de la misma.

Para ello un método sencillo sería obtener un dark frame con la cámara, es decir una captura con el objetivo tapado y con una longitud de exposición considerable para asegurar la presencia de ruido de partida, o en su defecto una captura sobre una superficie de color liso, sin textura y con iluminación totalmente uniforme. El estudio se hará para todos los valores ISO posibles.

Hecho esto analizaríamos con la FFT el resultado de un revelado totalmente neutro de los archivos RAW o mejor aún, de una extracción RAW pura de los canales R, G₁, G₂ y B. Ambos procesos pueden llevarse a cabo con DCRAW.

Como no dispongo de ninguna cámara que realice un preprocesado del archivo RAW, he generado un parche de color gris 128 al que he añadido ruido gaussiano en Photoshop.

Al aplicarle la FFT puede verse como aparece una delta en el origen (punto blanco) correspondiente al valor medio del parche, rodeada de valores espúreos de menor amplitud y sin apenas correlación espacial que corresponden al ruido introducido:


Fig. 15 Parche con ruido gaussiano (izq.) y su FFT (der.).

Veamos cómo queda alterada la FFT al aplicar diferentes reducciones de ruido sobre el parche de ruido gaussiano, siempre partiendo del original. Los resultados de la FFT se han ajustado en niveles para hacer más visibles los patrones geométricos obtenidos:

REDUCIR RUIDO (INTENSIDAD 5, COLOR 50%)

Podemos ver un patrón espacial claro que da indicios de la aplicación de un proceso de filtrado paso bajo en un entorno circundante a cada píxel.

Además parece que se trata de un filtrado más fuerte en las direcciones diagonales que en sentido horizontal o vertical:


Fig. 16 Reducir ruido en PS.

MEDIANA (DE 2 y 4 PÍXELES)

En este caso podemos ver cómo el filtrado de mediana se concentra fundamentalmente en la fila y columna donde se haya cada píxel, eliminando casi totalmente componentes frecuenciales en cualquier otra dirección.

A mayor radio de mediana más "armónicos" presenta la FFT, fruto del mayor período espacial de las operaciones efectuadas (menor frecuencia espacial):


Fig. 17 Mediana en PS (de 2 y 4 píxeles).

DESENFOQUE GAUSSIANO (DE 1 PÍXEL)

Como era de esperar el desenfoque gaussiano se traduce en un efecto paso bajo uniforme en todas las direcciones radiales alrededor de cada píxel afectado:


Fig. 18 Desenfoque gaussiano en PS.

DESENFOQUE DE LENTE (DE 6 y 8 HOJAS)

Aunque no son propiamente procesos de reducción de ruido, los desenfoques de lente son los más divertidos y gráficos de analizar.

Podemos ver en los claros patrones hexagonales y octogonales alderedor de cada píxel que el desenfoque de lente de PS, lejos de ser una falacia, sí parece actuar emulando un diafragma del número de hojas pasado como parámetro:


Fig. 19 Desenfoque de lente en PS (de 6 y 8 hojas).

~~~
Como puede verse a la FFT no se le escapa ni una. Para llevar a cabo este tipo de hallazgos sobre imágenes reales de terceras personas, bastará encontrar en las mismas una porción de color liso y sin textura y aplicar sobre ella el cálculo de la FFT.

En particular realizando este análisis sobre imágenes encontradas en los foros de la Sony A900, no me ha sido complicado hallar evidencias de procesado software cuando no era esperable o deseable encontrarlo.

CONCLUSIONES

Pese a no ser el mundo de la imagen un campo especialmente propicio para hallar aplicaciones a la FFT, en esta ocasión se ha revelado como verdaderamente útil para la eliminación de patrones periódicos en imágenes.

Los resultados obtenidos han sido francamente buenos aunque como se ha dicho ya la complejidad del procesado ha sido baja por la alta frecuencia espacial del patrón a eliminar. Es decir, aunque suene paradójico es más fácil y preciso eliminar tramados más finos que tramados más gruesos y distanciados.

La eliminación de este tipo de tramados nos permite disfrutar de texturas que de otro modo se hallaban ocultas o poco visibles debido precisamente a la interferencia. Es por ello que creo que este destramado debiera ser el primer paso a aplicar en cualquier proceso de edición/restauración de fotografía afectada por una trama periódica de este tipo.

También se ha introducido la FFT como herramienta útil para hallar evidencias sobre reducciones de ruido y otros procesados "clandestinos", llevados a cabo por ejemplo por una cámara sobre sus propios archivos RAW.


~~~

Si este contenido te ha resultado útil, considera realizar una contribución para asegurar la continuidad de esta web. Mantenerla supone un importante esfuerzo, así como un espacio y ancho de banda considerables en el servidor. Es una operación sencilla y totalmente segura.